计算机是现代社会处理信息的重要工具，而处理信息的基础就是存储信息。我们知道，现代计算机都用二进制来存储数据（只有两种状态的电子元件很容易制造）。但是我们现实生活中很少接触二进制，我们接触的大部分数据都是文字，或者十进制数字等等。而计算机需要用0，1的方式来表示出我们生活中各种各样的信息，这就需要我们了解如何将我们常用信息转化为0，1表示的形式。

在本文中，主要研究的是十进制转二进制的方法。

1.十进制转二进制：

我们生活中所使用的数字一般是十进制数。所谓十进制，就是一个逢十进一的数字系统，想必大家都很清楚，我就不赘述了。

类比十进制，二进制就是一种逢二进一的数字系统，这也就意味着二进制数中只会出现0，1两种数字。

相应的，它和十进制一样，都可以用来表示一个数字的大小，只不过位数比十进制位数要长而已。

我们重点关注的是十进制如何转化为二进制的。

一般地，我们一般用除二取余法把十进制转化为二进制。

在十进制中，我们不难发现，任何一个数字都可以表示为：

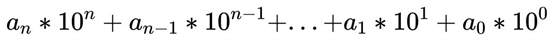
我们如果想要求出10进制中的每一个位上的数字，就可以运用除十取余，这样的话，第一个出现的余数就是a0，之后减去这个余数a0 再让这个数除10后取余数a1。

重复上述步骤，一步一步就可以得到每一位上的值。最后我们把an 到a0依次写出来，就得到了它原来的数。

模拟十进制表示的方法，我们对于每一个数同样可以写成一串二的幂相乘的形式：

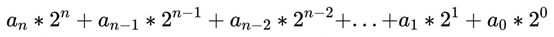
所以我们同样可以用除2取余法获得这个数字的每一个二进制位。

我们来举个例子，比如我们想要将521这个十进制表示数转换为二进制码的形式：

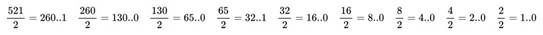
我们从最后一次除法得到的结果开始写（但是如果最后一次除法结果0，就直接从余数开始写），后面每一位都是上一次除二后的余数，让前面的余数依次排列得到1000001001这串数列（我们先得到的余数需要后写上，因为先得到的余数代表的低位上的值，而我们的习惯是先写高位后写低位）。

这样的话我们就得到了521这个十进制数的二进制表示：1000001001

2.小数的二进制表示：

我们同样可以通过类比十进制的方式来把小数转换成二进制。

我们发现，十进制的小数可以被表示为下面的表达式：

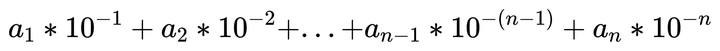
我们发现，我们将这个数乘10，那么我们会得到一个大于0小于10 的整数，这个整数就是a1。

根据这个表达式，我们只需要将这个数字乘10后取走个位（将个位减去），再乘10取走个位。以此类推，我们把每次取走的数拼起来，就得到了这个小数的值，即:

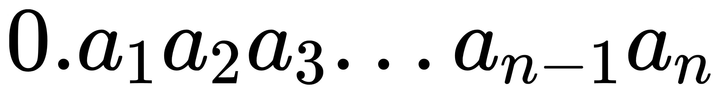
我们称这种方法叫做乘10取整法。

同样，一个小数当然也可以写成这种形式：

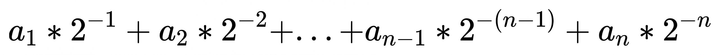
我们效仿计算10进制的小数的方式，进行乘2取整，每次将小数乘2，然后取走整数部分（只可能是1或0）。最后将取走的数字顺序依次拼在一起，就可以得到这个小数的二进制表达方式。

为了更好的理解，我们可以用一个具体的例子来表示一下，比如计算0.875的二进制小数表达式：

所以0.875的二进制就可以表示为0.111，注意，此处第一个拿出来的1放在序列的最前方，越是优先的得到的数，排的越靠前。这里和整数的除二取余法有些不同。

注意：因为二进制的特殊性，有很多有限的十进制小数在转换成二进制小数后会出现无限循环的现象，这是正常的，在计算机中会被限制在一定长度后舍入。

我们在求一个既有整数也有小数的数的二进制表示时，可以先将小数和整数拆开，然后分别计算，最终将得到的结果拼在一起得到这个数的完整二进制码。

所有的数都可以用二进制码的形式表示出来，这也给二进制计算机存储数据奠定了基础。