极坐标算面积公式, 建极坐标系解一道圆锥曲线大题,解法参考。圆锥曲线中求最值
100次浏览
发布时间:2024-07-20 10:01:35
编辑: 良知花
建极坐标系解一道圆锥曲线大题,解法参考。
这道题求三角形面积的最大值和最小值,计算会有点繁琐,也很难搞明白哪种情况下三角形面积取得最大最小值,对于大部分高中学生来说,这是一道难题。
请读者先尝试完成,再看解答。如果不用极坐标系,怎么求解?
2021年高考数学圆锥曲线大题解法参考,以及与课本原型的对比
一,请看题:

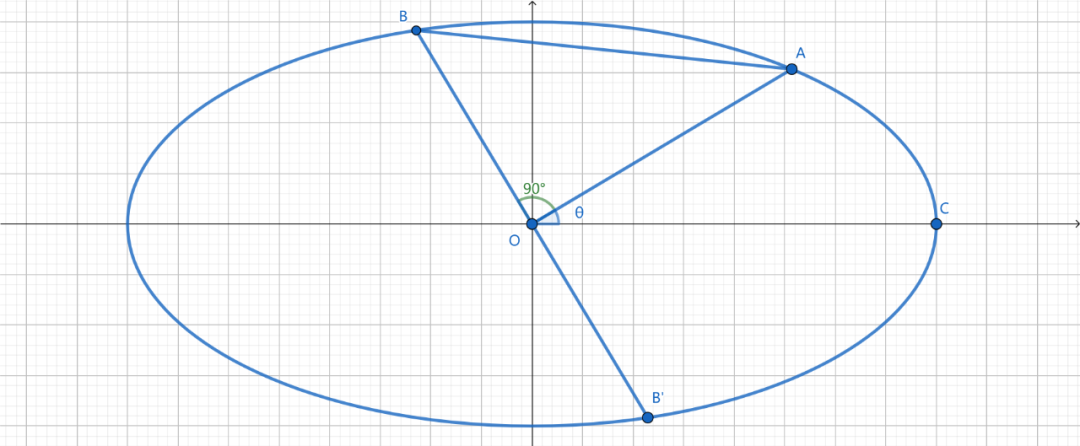
二,建立极坐标系解题,解法参考。
有关极坐标系的知识点,属于高中数学的选修内容。对于学好高中数学,其中一个方法,就是把老版本教材的选修内容,也当成必修内容去学一遍,把刷题时间抽出一小部分来学习选修内容,是非常划得来的。
第1问,解法参考:

第2问,解法参考:
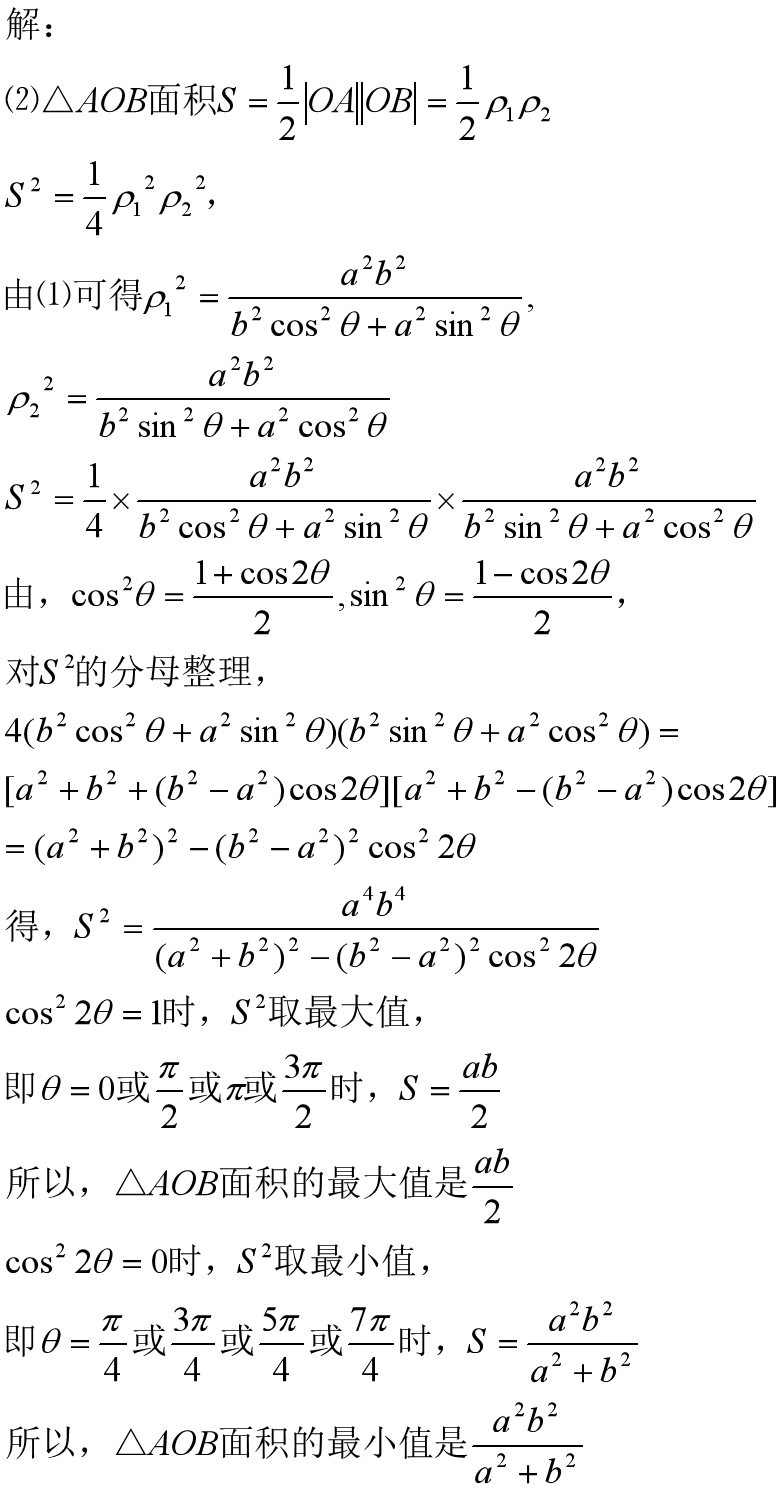
三,极坐标系。
如图,在平面内取一个定点O,叫做极点;自极点O引一条射线Ox,叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方面(通常取逆时针方向),这样就建立了一个极坐标系。
设M是平面内一点,极点O与点M的距离OM叫做点M的极径,记为ρ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记为θ。有序数对(ρ,θ)叫做点M的极坐标,记为M(ρ,θ)。